SRP i matematik og fysik om raketvidenskab

Introduktion

Mekanik er en disciplin inden for fysikken som kort sagt handler om, hvordan ting bevæger sig. I mekanik stilles spørgsmålet: hvis vi kender de kræfter, der påvirker et givet legeme, og vi kender legemets bevægelse (dvs. position og hastighed) i et givet øjeblik, kan vi da forudsige, hvordan legemet vil bevæge sig? Svaret er i princippet "ja", og dette skyldes i høj grad teorien udviklet af den engelske fysiker og matematiker Isaac Newton (1642-1727). Denne teori er kendt som den klassiske mekanik. En af Newtons store bedrifter var en ganske nøjagtig beskrivelse himmellegemernes bevægelser (Månen, planeter, kometer osv.). Han indså som den første at bevægelserne var forårsaget af den samme kraft (tyngdekraften), som fx får en bold til at falde til jorden, når man slipper den. En af menneskehedens store bedrifter videnskabeligt og teknologisk set er at have landet et bemandet fartøj på Månen. En væsentlig del af teorien der ligger til grund for denne bedrift - og for hele videnskaben om raketter og rumfart - er stadig den dag i dag Newtons love.    

Det er næppe realistisk at sende en raket til Månen, men i dette projekt vil vi alligevel se på den bagvedliggende matematik og undersøge nogle af de samme lovmæssigheder, der gælder for en rigtig rumraket.  

Projektbeskrivelse

For at give et indtryk af teorien i projektet vil vi her udlede raketligningen som beskriver, hvordan rakettens fart udvikler sig. Hvis man ønsker, at raketten opnår en given fart, må man kontrollere hvor hurtigt brændstoffet stødes ud af raketten. Det er nemlig sådan raketten drives fremad. Dens bevægelse er en rekylbevægelse ligesom en pistol der stødes bagud, idet kuglen affyres. Raketligningen fortæller også på hvilken måde rakettens endelige fart afhænger af, hvor stor en del af rakettens masse der er brændstof. 

I det simplest mulige tilfælde ser vi bort fra eventuel luftmodstand og antager at raketten ikke er påvirket af (fx Jordens eller Månens) tyngdekraft. Vi betegner rakettens masse inklusiv brændstof med $m$ og dens fart til et givet tidspunkt med $v$. Rakettens bevægelsesmængde (også til tider kaldet impuls) er således $mv$. Antag, at der i dette øjeblik udstødes en mængde brændstof, og at rakettens masse derefter er $m+dm$. Heri ligger altså dels at $dm$ må være et negativt tal, dels at brændstofmængden har masse $-dm$. Rakettens fart efter udstødning er $v+dv$, og vi betegner den hastighed hvormed brændstoffet udstødes i forhold til raketten med $u$. Bevarelsessætningen for bevægelsesmængde (også kaldet impulsbevarelsen) siger at bevægelsesmængden er den samme før og efter udstødningen. Situationen er illustreret på tegningen nedenfor.

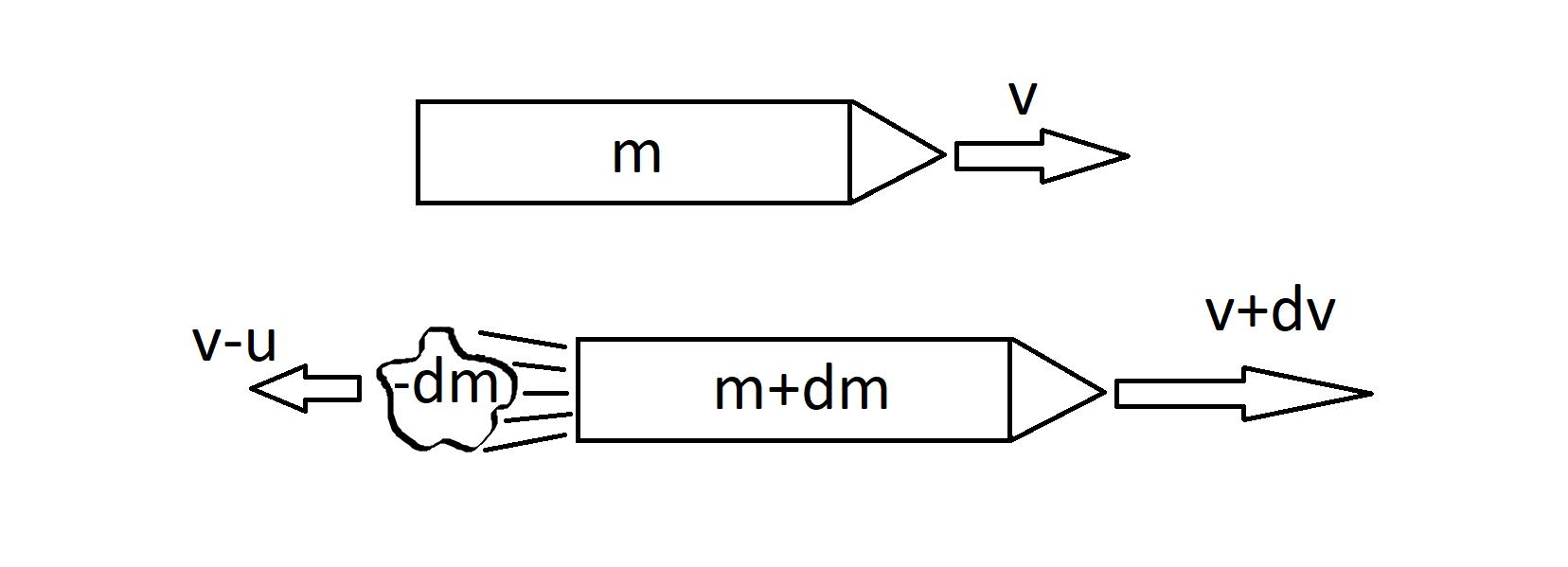
Bevarelsessætningen kræver altså at

$$mv = (m+dm)(v+dv)+(v-u)(-dm)$$

Vi antager at $dm$ og $dv$ er meget små størrelser, sådan at når vi ganger parenteserne på højresiden ud, kan vi se bort fra leddet $dmdv$. Derved reducerer ligningen til

$$dv=-\frac{u}{m}dm$$

Ved separation af variable fås

$$\int dv=-\int\frac{u}{m}dm$$

Vi integrerer og får

$$v=-u\ln(m)+c$$

hvor $c$ er en konstant. Hvis vi betegner rakettens fart umiddelbart inden udstødningen med $v_0$ og dens masse med $m_0$, får vi at 

$$c=u\ln(m_0)+v_0$$

og dermed har vi raketligningen:

$$v=u\ln\left(\frac{m_0}{m}\right)+v_0$$

Raketligningen kan testes på en vandraket som i stedet for brændstof bruger vand under tryk. Eksperimenter af denne type bliver ofte lavet i gymnasiefysik, så din skole har måske allerede en vandraket liggende. Her følger nogle ideer til videre arbejde i projektet.

Man kan udregne hvor højt raketten kommer op og sammenligne med forsøgsresultater. I den forbindelse bliver det relevant at inkludere tyngdekraften og luftmodstand i ligningerne. Man kan også forsøge at udregne udstrømningshastigheden for vandet i raketten som funktion af tiden. Endnu en mulighed er at beregne den optimale mængde vand i raketten (dvs. den mængde der gør at raketten kommer højest) og teste resultaterne eksperimentelt. Langt de fleste veje igennem projektet vil desuden matematisk set kræve numerisk integration i forbindelse med løsning af diverse differentialligninger. Der findes mere eller mere avancerede metoder til dette, fx Eulers metode eller mere generelt Runge-Kuttas metode(r). 

Eksperimentelt set kan man forsøge sig med en opstilling, hvor raketten overfører sin kraft til en opstillet plade - en kraftmåler af en slags (måske en vægt) - og sammenligne resultaterne med en beregnet kraft. Det er også oplagt at filme raketten når den er i luften med henblik på at analysere bevægelsen efterfølgende. Det er dog også vanskeligt i praksis, da raketten kan komme ganske højt op. Har man lyst til en mere praktisk udfordring, er det altså noget at overveje her. Det er også en mulighed at bruge luft i stedet for vand som "brændstof", og man kan måske også eksperimente med andre væsker end vand.  

Materialer

Andersen F., Bostrup O., Halkjær E. & Hansen K.G.: "Fysik for gymnasiet 2", Gyldendal, 2.udg., 1972 (s. 81-83). 

Christensen C., Clausen C. & Felsager B.: "Fysikkens Spor", Gyldendal, 1990 (s. 20-23).

Holm P.: "Raketter", Gyldendal, 1974. (Bemærk: indeholder også relevant matematik i appendix.

Ingwersen J., Jensen H. B. & Sørensen K.E.: "Kernestoffet - højt niveau", Systime, 1980 (s. 26-28). 

Kleppner, Daniel m.fl.: "An introduction to mechanics", McGraw-Hill, 1987.

Knudsen J. M.: "Elements of Newtonian Mechanics", Springer, 2002 (s. 57-61). 

Pihl M. & Henning S.: "Fysik 3", GAD, 1974, (s. 131-134). 

Staffanson, E. m.fl.: "Fysik i grundtræk 2A", Munksgaard, 1973 (s. 92-99).