SRP i matematik og kemi om knudeteori
Introduktion
I dette projekt undersøges brugen af knudeteori i kemien. Knudeteori er en del af et større matematisk felt kaldet topologi. I topologien studerer man geometriske former med særligt fokus på de egenskaber ved formerne som ikke ændrer sig, når formen ændres under en såkaldt kontinuert deformation. For at gøre dette mere forståeligt kan vi betragte en konkret geometrisk form, fx en cirkel. Hvis vi tænker på cirklen som en snor, kan vi ved at flytte lidt på snoren omdanne den til fx en trekant. Dette kan vel at mærke gøres uden at klippe snoren over eller binde eventuelle løse ender sammen, og dette er den intuitive forståelse af en kontinuert deformation. Selvom en cirkel og en trekant er geometrisk forskellige former, vil man i topologien betragte dem som én og samme form. Klipper vi snoren over (hvilket altså ikke er tilladt under en kontinuert deformation), får vi et linjestykke. En cirkel og et linjestykke er topologisk set forskellige former, da den ene ikke kan deformeres kontinuert over i den anden. Et andet eksempel ses på figuren nedenfor. Cirklen (A) og trekanten (B) er som nævnt topologisk set ens, men man kan ikke deformere nogen af dem over i den tredje figur (C) uden at klippe snoren over og binde den sammen igen. På figur C er der med andre ord en knude på snoren som ikke kan løses. Der er altså en grundlæggende forskel på formerne A og C. Om der "er knude på" snoren eller ej, er således et topologisk spørgsmål. I kemiens verden findes en række molekyler som danner knuder, og dermed bliver knudeteori et relevant værktøj, når det handler om at forstå sådanne molekylers struktur.
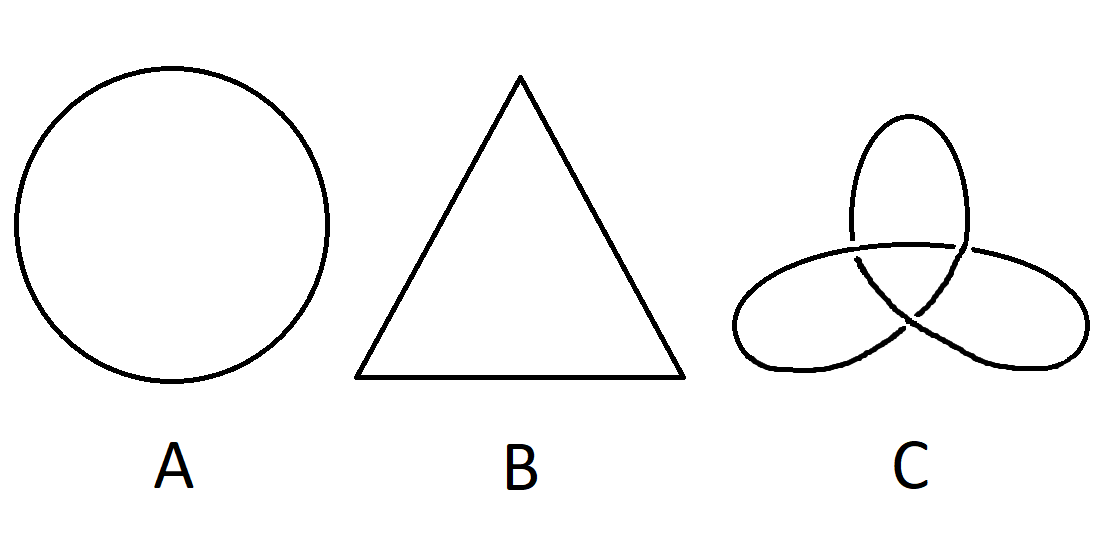
Projektbeskrivelse
Projektet kan tage sit udgangspunkt i den matematiske definition af en knude. For at gøre tingene enklere kan en knude eventuelt betragtes som en lukket kæde af liniestykker i det 3-dimensionelle rum. Derfra kan man gå videre til knudediagrammer og Reidemeisters sætning som eventuelt kan bevises. Desuden kan simple (pseudo)invarianter omtales: trefarvning, vridetal, krydsningstal. Andre relevante begreber kunne være:
- Splejsning og disjunkt forening.
- Pindetallet (stick-number).
- Jones-polynomier.
- Jones-polynomier for givne simple knuder.
- Vasiliev-invarianter.
Udregningerne af Jones-polynomier kan automatiseres vedhjælp af CAS-værktøjer (der er tale om en rekursiv udregning ved brug af en såkaldt garnnøglerelation).
Alternativt kan man betragte fletninger i stedet for knuder, da disse involverer mange af de samme begreber. Fordelen ved fletninger er at de besidder en gruppestruktur: den fri gruppe med frembringere, hvor er antallet af snore i fletningen.
Fra det kemifaglige perspektiv kan knudeteorien anvendes som modelleringsværktøj. En mulig problemstilling er at give eksempler på cykliske molekyler samt at beskrive hvor mange forskellige måder de kan forgrenes på (her kommer pindetallet ind i billedet). Hvilken kemisk betydning har knuden? En anden mulighed er at sammenligne DNA-molekylets mutationer med splejsning af knuder.
Materialer
Hansen, Kenneth: "Knudeteori", Systime, 1998.
Sossinsky, Alexei: "Knots – mathematics with a twist", Harvard University Press. 2004.
http://pass.maths.org.uk/issue15/features/knots/index.html (Om brugen af knuder i kemi. Let og underholdende læsning. Omtaler pindetallet og torusknuder).
http://www.ams.org/featurecolumn/archive/knots-dna.html (Om Jones-polynomiet og dets anvendelse. Mange illustrative figurer og referencer til bøger om generel knudeteori og om brugen i kemi og biologi).
