Studieretningsprojekt i matematik og biologi om epidemimodeller

Introduktion

Projektet omhandler epidemiske sygdomme, de biologiske og sundhedsmæssige aspekter af disse samt hvordan matematik kan anvendes til at opstille en model for udviklingen af en epidemi. De biologiske aspekter vil særligt være smitsomme sygdomme, det menneskelige immunsystem, samt teori om og eksempler på epidemiers forløb. De matematiske aspekter er særligt epidemimodellen SIR i forskellige varianter. Desuden kan inddrages analyse af statistiske data fra faktiske epidemier, sammenligning af data med modeller og muligheder for forbedring af modeller.

Eventuelt kan faget historie også inddrages med fokus fx på samfundsmæssige faktorer, der påvirkede epidemiens forløb, og/eller de konsekvenser epidemien havde på de berørte samfund/mennesker/områder.

Virus-SIR

Projektbeskrivelse

I det følgende gives en kort introduktion til SIR-modellen. Der gøres nogle grundantagelser:

Antallet $N$ af individer i befolkningsgruppen er konstant. Altså ses der bort fra nyfødte og immigranter, og afdøde individer tælles stadig med.
Der er tale om en homogen interaktion mellem individerne, dvs. at alle med lige stor sandsynlighed kan støde ind i hinanden.
Individer der har haft sygdommen, men som er blevet raske, bliver immune og kan altså ikke blive syge igen.

Befolkningsgruppen inddeles i tre disjunkte grupper til tiden $t$:

$S_t$: Antallet af raske individer der er modtagelige for sygdommen (suspectible).
$I_t$: Antallet af smittede individer (infective).
$R_t$: Antallet af individer der er immune, fordi de har haft sygdommen (removed). Bemærk, at individer der er døde af sygdommen, tælles med i $R_t$.

Da populationsstørrelsen $N$ er konstant, gælder der for alle $t$, at $N = S_t + I_t + R_t$. Et individ, som rammes af sygdommen, kan derfor siges at bevæge sig mellem de tre grupper på følgende måde:

$$S \longrightarrow I \longrightarrow R$$

Følgende tre differensligninger kan opstilles for at beskrive dynamikken mellem de tre grupper:

\[
\begin{align}
S_{t+1} &= S_t - \alpha S_tI_t\\
I_{t+1} &= I_t + αS_tI_t - \gamma I_t\\
R_{t+1} &= R_t + \gamma I_t
\end{align}
\]

Her kaldes koefficienten $\alpha$ for transmissionskoefficienten, og den fortæller noget om sandsynligheden for, at et individ i den modtagelige gruppe bliver smittet ved mødet med en allerede inficeret person. Koefficienten $\gamma$ er den såkaldte removal rate, og den rummer information om antallet af inficerede individer, der kureres af sygdommen eller dør indenfor et givet tidsinterval.

Tilvæksten over et tidsinterval for de forskellige kategorier kan opskrives som:

\[
\begin{align}
\Delta S &= -\alpha S_tI_t\\
\Delta I &= \alpha S_tI_t - \gamma I_t = \alpha I_t(S_t - \rho)\\
\Delta R &= \gamma I_t
\end{align}
\]

Her er $\rho = \gamma /\alpha$ den såkaldte relative removal rate, som er et vigtigt begreb, idet den kan opfattes som en slags tærskel, hvor epidemien topper. Der gælder nemlig, at hvis $\Delta I > 0$, så opstår der en epidemi, idet tallet af inficerede vil vokse. Hvis der derimod gælder $\Delta I \leq 0$ for alle $t$, så er der ikke fare for epidemiudbrud. Idet transmissionskoefficenten $\alpha$ er et positivt tal, får vi nemlig fra ligningen $\Delta I = \alpha I_t(S_t - \rho)$, at hvis $S_t > \rho$, så er $\Delta I> 0$, og hvis $S_t \leq \rho$, så er $\Delta I \leq 0$. På figuren nedenfor er $S_t, I_t$ og $R_t$ vist som funktion af $t$ ($S_t$=blå, $I_t$=rød, $R_t$=grøn):

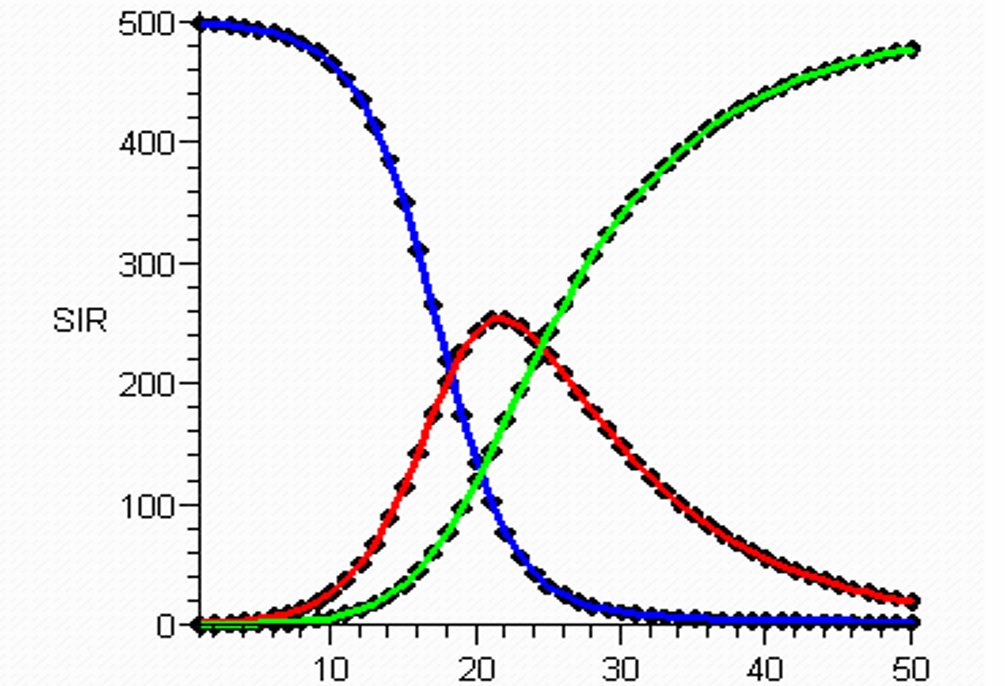
SIR-model

Parameteren $\rho$ kan estimeres ved aflæsning. Når epidemien topper, går $\Delta I$ nemlig fra at være positiv til at være negativ. Toppunktet for kurven for $I_t$ har toppunkt når $\Delta I = 0$, og for dette $t$ kan man aflæse værdien $S_t = \rho$. Denne værdi siger os noget om, hvor voldsom epidemien vil være. Man kan også aflæse $\rho$ ud fra $SI$-fasediagrammet. Dette diagram viser den parametriserede kurve $(S_t,I_t)$:

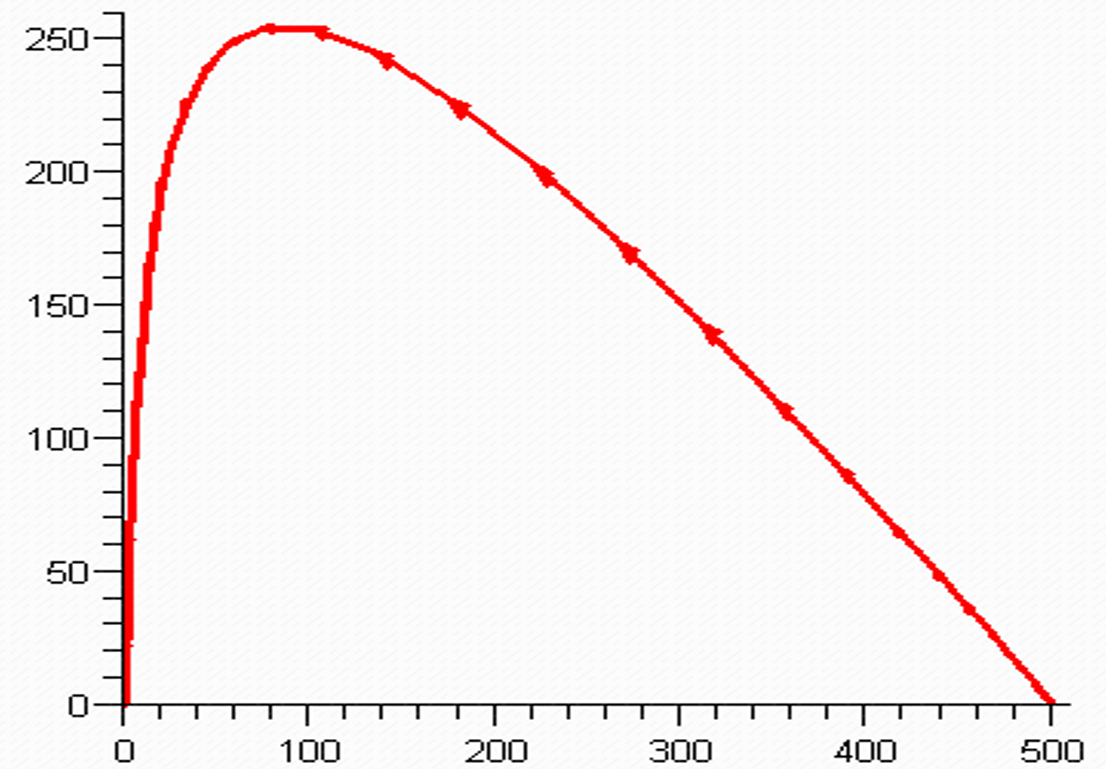
SIR-fasediagram

Toppunktet for grafen er $(\rho, I_{max})$, hvor $I_{max}$ er det maksimale antal inficerede under epidemien. Endvidere kan $\alpha$ estimeres ud fra $\gamma$ og $\rho$ ved at udregne $\alpha =\gamma / \rho$.

Hvis vi igen betragter $\Delta I_t = \alpha S_tI_t - \gamma I_t = \gamma I_t (\alpha /\gamma S_t -1)$, så er en anden vigtig størrelse $R_0 = \alpha /\gamma S_t = (\alpha S_t)(1/\gamma)$, som kaldes basic reproduction number. Ud fra højre side af lighedstegnet ses at $R_0$ fortæller, hvor mange personer en inficeret person når at smitte i løbet af smitteperioden. Her er $R_0= 1$ en tærskel, idet der gælder, at hvis $R_0> 1$, så er $\Delta I > 0$, og en epidemi vil forekomme, mens $R_0 \leq 1$ vil medføre at $\Delta I \leq 0$. Dette betyder at hvis sundhedsmæssige tiltag kan sikre, at antallet af modtagelige personer er mindre end den relative removal rate, dvs. $S_0< \rho$, så vil dette forhindre epidemien at bryde ud.

Et uventet resultat af SIR-modellen er, at det som regel vil gælde, at grænseværdien for $S_t$ for $t\to\infty$ ikke vil være 0. Der altså modtagelige personer, som aldrig vil blive smittet.

Variationer og modifikationer af modellen

Her omtales hvordan man eventuelt kan tilpasse SIR-modellen til forskellige sygdommes forløb.

SI-model: De inficerede kan ikke blive raske igen (fx AIDS).
SIS-model: Hvis en inficeret person bliver rask, så er vedkommende igen modtagelig for sygdommen. Det er altså ikke muligt at blive immun (fx syfilis eller lus).
sir-model: I stedet for at betragte absolutte tal kan det ofte være belejligt at se på procentdele af befolkningen. Her er $s=S/N, i=I/N$ og $r=R/N$.
SIRS-model: Her forsvinder immuniteten med årene, og en person risikerer derfor at blive syg igen senere i sit liv.

Desuden kan man tage hensyn til nogle af de antagelser, som blev nævnt i starten. Eksempelvis kunne man inkludere en parameter for fødsler/dødsfald i modellen.

En anvendelse af sir-modellen kan sikre, at der aldrig vil være mere en vis procentdel af befolkningen, som bliver inficerede. Hvis vi antager, at $i_0$ er andelen af inficerede til tiden $t=0$, og det ønskes at andelen ikke skal vokse, så skal man sørge for at $\Delta I<0$. I sir-modellen er

$$\Delta i=\beta s_t i_t-\gamma i_t=(\beta s_t-\gamma ) i_t =\beta (s_t-\gamma / \beta ) i_t$$

Her kaldes koefficienten $\beta$ for kontaktraten. Da $i_t$ og $\beta$ begge antager værdier mellem 0 og 1, så er kravet altså at $s_0 < \gamma / \beta=1/\sigma$, hvor $\sigma$ kaldes kontakttallet. Man kan derfor konkludere, at hvis man sørger for at andelen $1-1/\sigma$ af befolkningen er immune, så er der ifølge sir-modellen ikke risiko for en epidemi.

Problematiske aspekter

Foruden de antagelser der blev formuleret i starten, tager SIR-modellen heller ikke højde for faktorer som

hvilken aldersgruppe individerne tilhører
hvilket køn individerne tilhører
hvilket socialt lag individerne tilhører
individernes helbredsmæssige status

Variationsmuligheder

Matematik

Der er mulighed for at benytte forskellige modifikationer af SIR-modellen til at beskrive forskellige slags sygdomme, og der findes forskellige måder at anvende computerprogrammer til at simulere sygdomsforløbene. Det er måske også muligt at benytte sig af helt andre modeller.

Biologi

Der kan arbejdes med forskellige smitsomme sygdomme, og data fra epidemiforløb kan varieres. Der kan arbejdes med sygdomme med forskellige karakteristika, fx en sygdom med/uden resistensudvikling.

Eksempler på problemformuleringer

Opgave I
Der ønskes en kort redegørelse for det menneskelige immunforsvar. Beskriv i den forbindelse smitsomme sygdomme fremkaldt af mikroorganismer og den biologiske baggrund for udvikling af resistens overfor smitsomme sygdomme.

På baggrund af dette ønskes en redegørelse for SIR-modellen. Anvend modellen til at analysere det vedlagte datamateriale for (sygdom X).

Diskuter og vurder, hvad man på samfundsplan kan gøre, for at forhindre og begrænse udbrud af smitsomme sygdomme og hvordan matematiske modeller som SIR kan bruges i den forbindelse.

Opgave II
Der ønskes en redegørelse for den SIR-modelen for smitsomme sygdomme. Breskriv i den forbindelse relevante biologiske aspekter.

Anvend modellen til at udføre simuleringer over tid af epidemiforløb af sygdomme med forskellige biologiske egenskaber.

Diskuter de fremkomne epidemiforløb ud fra de matematiske og biologiske forudsætninger. Overvej muligheder for udvidelse og ændring af SIR-modellen med henblik på at simulere forskellige typer sygdom.

Materialer

Allman, E. og Rhodes, J.: ”Mathematical Models in Biology”, Cambridge University Press, 2004 (specielt kapitel 7).

Andreasen, Viggo: ”Introduktion til matematisk infektionsepidemiologi”, IMFUFA (RUC), 2004. PDF-udgave: http://uvmat.dk/paradig/not/n215-1.pdf .